A minimum complete introduction to ESA's Euclid Mission
Introduction
Euclid is a pretty amazing space mission like many others. I challenge myself in this post, and I try to explain the Euclid mission. By using the Euclid mission as an example, I hope to say something new for anybody reading this post.
My other posts explaining something minimally but in a complete way are popular reads in this blog. I try to do the same here. I will tell you about the Euclid mission, but when doing this, I will also explain the relevant terms or concepts as minimum but reasonably complete as possible. I usually write the main section without extra explanations, but then give more information in subsections; for example, I will explain Euclid Wide Survey assuming you know what $deg^2$ is, if you do not know what it is, you can learn about it in the following subsection.
This post is just a differently organized summary of various public information, according to my purpose of giving a minimum but a complete introduction. The main resources are given in References but mainly they are linked in the text. The original source of the images can always be directly reached by clicking on them.
If you are an expert on the topic and if you see something wrong in this post, please let me know.
Euclid Mission
Euclid is one of the two launched missions of European Space Agency (ESA) in 2023 (the other is Juice). It is launched just a few days ago, on the 1st of July, on a Space X Falcon 9 rocket from Cape Canaveral in Florida, USA.
Euclid mission is about understanding the nature of dark energy, dark matter and gravity. These can be studied by weak gravitational lensing by measuring the shape and photometric redshifts of distant galaxies and by galaxy clustering by measuring the spectroscopic redshifts. Euclid will measure all of these for more than 1/3 of the sky, effectively looking back up to 10 billion years ago.
Euclid (the ancient Greek mathematician) is considered as the father of geometry. As the mission is about the geometry of the space, it is named Euclid.
Cosmological Redshift
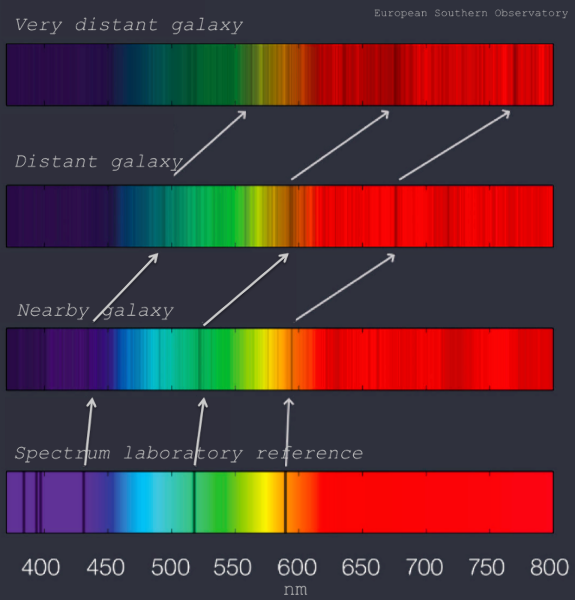
According to Hubble’s law, the further a galaxy is from the Earth, the faster it is moving away from the Earth. When an object is moving, the wavelength of sound or light wave they emit changes. You can observe this when a train is coming at its normal speed towards you, then going away from you. So, the faster a star is moving (towards the earth or away from the earth), its light will be seen as more off than it actually is; for example, if it emits a light at 600nm, it will be seen as 610nm from the Earth. Figure below shows that, the spectral line on the spectrum (meaning the wavelength of something emitted) in a stationary object is increased when the object is moving away.

Redshift (source: itu.physics.uiowa.edu)
According to Hubble’s law, the distance has a linear relationship with the velocity, and the velocity causes redshift. Neither the speed nor the distance of a galaxy can be directly measured. However, the amount of (red)shift (or blueshift) can be measured by spectroscopy, and the velocity and then the distance can be estimated. The figure below shows the increasing amount of redshift depending on the distance of the galaxy.
Redshift vs. Distance (source: itu.physics.uiowa.edu)
The amount of redshift is quantified with redshift parameter z. With “rest” meaning the object is not moving, and “v” meaning the velocity of the object:
$z = \frac{\Delta\lambda}{\lambda_{rest}} = \frac{\lambda_{observed} - \lambda_{rest}}{\lambda_{rest}} = \frac{v}{c}$
When a star is travelling towards the Earth, observed wavelength is smaller than the rest, so z is negative. This is called blueshift. If it is travelling away from the Earth, than observed wavelength is larger, and z is positive. Due to the expansion of the universe, things are usually moving away from each, so it is usually redshift not blueshift.
Euclid will be able to measure galaxies having z=2, it means the light has been travelling for more than 10 billion years. The actual distance to the object now is more than this, more than 15 billion light years.
Expansion of the Universe
The expansion of the universe means the unit of scale on large scales (e.g., among galaxies) are expanding. For example, the distance between the star A and star B was 1 light years some time ago, but it is now 1.1 light years. This cannot be observed in small scales (e.g., between my keyboard and mouse), because the effect will be very small, and there are other forces stronger than what causes the expansion.
It is believed that there was a sudden and huge expansion after the Big Bang, and then it continued at a much slower pace. However, around 4 billion years ago (~10 billion years after the Big Bang), the expansion started to increase its pace. At the moment, it is estimated to be around 70 km/s per megaparsec. For example, Polaris is approx. 132 parsec away, this makes the expansion at approx. 9 km/s. So, Polaris is moving away from us at a speed of 9 km/s.
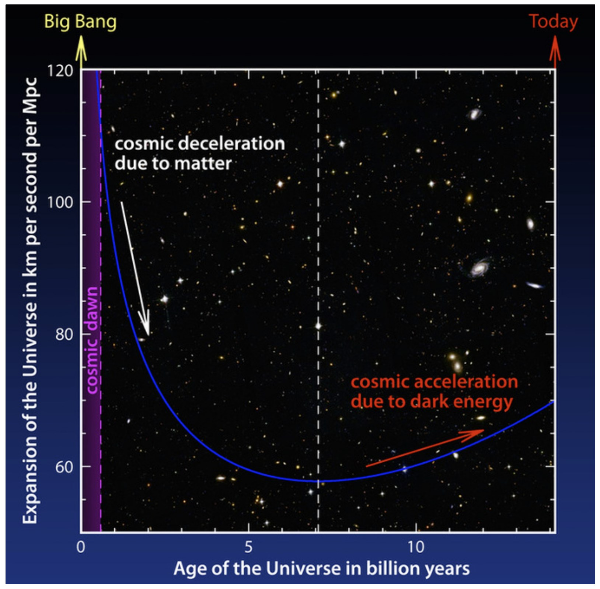
(source: euclid.caltech.edu)
This is difficult to imagine, since normally if something moves something else takes its place. However, the expansion of the universe is not of that kind. Nothing takes place of the objects moved apart, instead, it is like the space growed while objects are standing still.
The distance between the objects in space cannot be directly measured, so to study the expansion of the universe, redshift is observed.
Weak Gravitational Lensing
Weak Gravitational Lensing is basically the change or distortion of the appearance of objects due to the deflection of light due to a large mass. This is measured by analyzing the location and the shape of objects by photometry and their distance by measuring the redshift with spectroscopy.
Probably the first weak gravitational lensing measurement was the Eddington Experiment to test the Einstein’s general theory of relativity theory.
Galaxy Clustering
Galaxy clustering is the (3D) distribution of galaxies in the sky. It is measured by the angular position and the distance of galaxies (by measuring redshifts). By looking at the distribution, various cosmological properties can be studied.
Surveys and Fields
Euclid will complete two surveys during its operation: Wide and Deep. Survey means it is going to observe (or take an image both in visual and infrared bands) (a part of) the sky.
Euclid Wide Survey (EWS)
Euclid will capture $15000\ deg^2$ of sky during its 6 years mission. This is just a bit more than one third (1/3) of the whole sky. This is called the Euclid Wide Survey (EWS).
For EWS, an area of $0.57\ deg^2$ will be observed almost every hour. This is almost three times the area of full moon in the sky, which is about $0.2\ deg^2$.
One third of the sky to be observed is not a single but four regions (of interest) as shown in blue in the figure below in galactic coordinates. These four regions are neither close to the solar system plane (the diagonal in the center, 60 degrees from the galactic plane) nor the Milky Way galactic plane (horizontal in the middle). The reason is that the Milky Way stars and the dust and gas in the Milky Way and in the solar system decreases the quality of the observations. Since the aim of the mission is to observe distant galaxies, the four regions are selected to be not near to those areas.
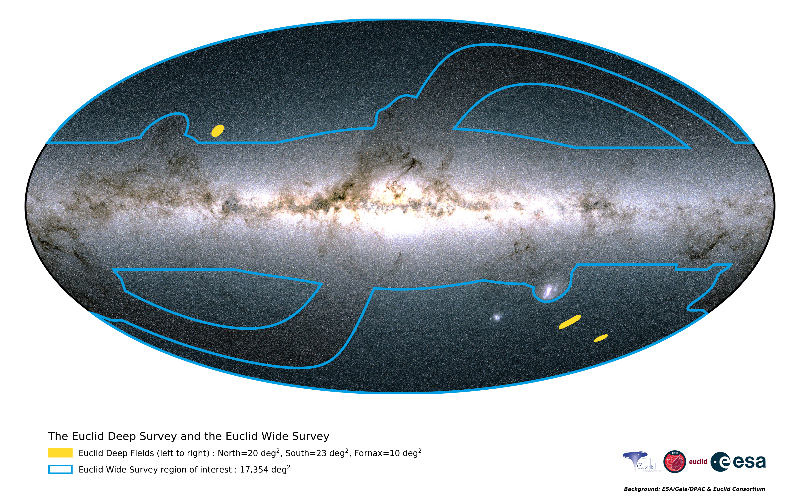
Euclid Wide Survey Regions and Euclid Deep Fields (source: ESA)
The survey will be completed in 6 years. The figure below shows a planning done in 2022 (I dont know yet if this is the final plan), showing which areas will be observed every year in different shades of blue.
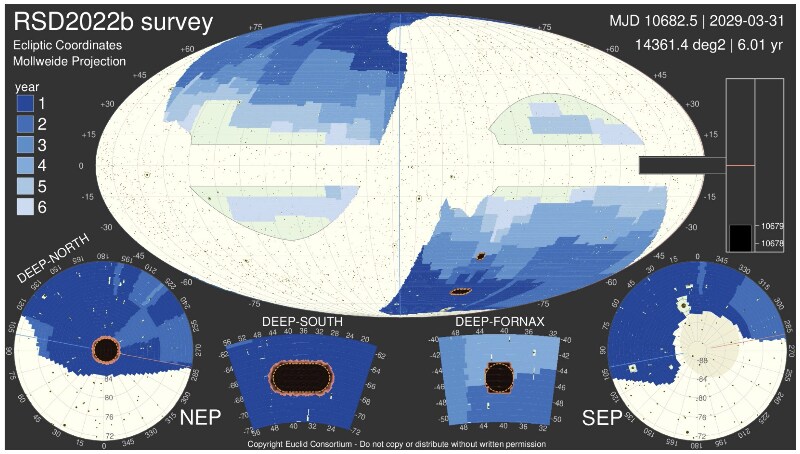
Reference Survey Definition 2022B
(source: Medinaceli, E. et al. 2022)
Solid Angle $\Omega$ and $deg^2$
In 3D, the field of view is measured with a solid angle, which has a unit of steradian (sr). 1 sr means a field of view looking at a surface area $r^2$ of a sphere with a diameter $r$. For example, assume you have a sphere with a diameter of $1\ m$, then $1\ sr$ sees a surface area of $1\ m^2$.
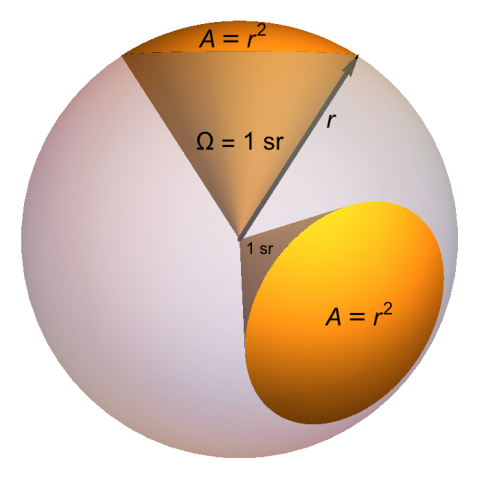
Solid Angle (source: wikipedia)
In degrees, $1\ sr = (\frac{180}{\pi})^2\ deg^2$
So, the whole sphere (whole sky) would be:
$4\pi\ sr = 4\pi(\frac{180}{\pi})^2\ deg^2 \approxeq 41200\ deg^2$
Galactic Coordinates
The center of the galactic coordinate system is the Sun. Its primary direction is to the approximate center of the Milky Way galaxy (Sagittarius A* (Sgr A*) black hole). Its fundamental plane is parallel to the (Milky Way) galactic plane and it is passing through the Sun (approx. 56.75 light years north of the galactic plane).
A galactic coordinate is given with:
Galactic longitude (l, in degrees): angular distance eastward (looking from the galactic north pole) between the galactic center and the object. It has no east-west distinction, the angle is from 0 to 360 degrees.
Galactic latitude (b, in degrees): angle between the galactic equator (galactic plane) and the object. It is positive above the galactic plane, thus it ranges from +90 degrees (the north galactic pole) to -90 degrees (the south galactic pole).
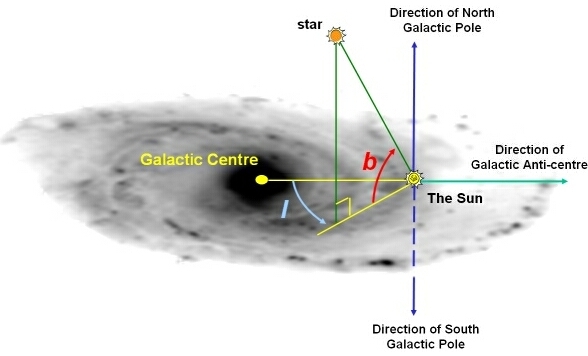
Galactic coordinates (source: astronomy.swin.edu.au)
Milky Way is basically a disc, whose diameter is almost 90K light years but it is only 1K light years (thin disk) to 10K light years (thick disk) thick.
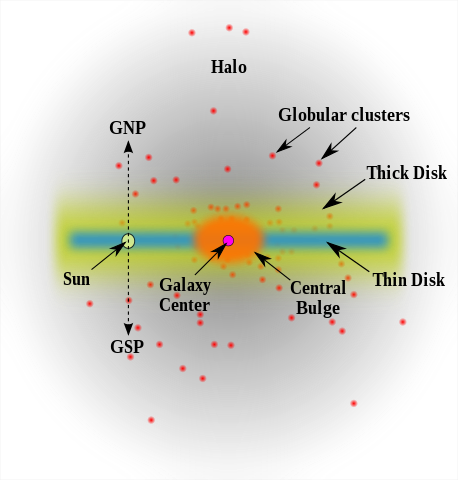
A schematic profile of the Milky Way (source: wikipedia)
The galactic coordinates of any object can be seen in Stellarium.
Euclid Deep Survey (EDS) and Euclid Deep Fields (EDFs)
Euclid will also observe a much smaller portion of the sky, only $53\ deg^2$ in total, but for much longer. This is called Euclid Deep Survey (EDS). This smaller portion of the sky consists of three regions (or fields), all of which are near to ecliptic poles (away from solar system plane), and these fields are called Euclid Deep Fields (EDFs). They are shown in yellow in the figure above and named: EDF-North, EDF-South and EDF-Fornax.
Being observed for much longer, EDS will capture much fainter galaxies than EWS. Each EDF will be observed different number of times:
- EDF-North (EDFN) covers $20\ deg^2$ and it will be visited 40 times.
- EDF-South (EDFS) covers $23\ deg^2$ and it will be visited 45 times.
- EDF-Fornax (EDFF) covers $10\ deg^2$ and it will be visited 52 times. 7 visits will be done within a few hours-days every ~9 months.
Also, in addition to “red” grism data as in EWS, “blue” grism data will be obtained for these fields during EDS. The “blue” grism data is not collected in EWS.
Because EDFs are also inside EWS, EDS will also be useful to assess the quality of EWS.
Euclid CPC and Euclid Auxiliary Fields (EAFS)
I am not sure what Euclid CPC Fields are for, but they coincide with the EDF-North and EDF-South, so they are not different than EDFs.
EAFs are used for calibration and there are seven EAFs.
Spacecraft
Euclid spacecraft is roughly 4.7m tall and 3.7m in diameter. It consists of two modules: Service Module (SVM) and Payload Module (PLM). These are connected in a way to minimize thermal coupling between them. It will be almost 2 tonnes in the orbit (800kg PLM, 850kg SVM, 40kg balancing mass, 210kg propellant).

Euclid spacecraft (source: ESA/SpaceX)
In the image above, the solar panels can be seen on the right, the telescope is inside the white cylinder on the left behind and the instruments are at the bottom section under the telescope.
SVM (Service Module)
Service Module contains the subsystems required to operate the payload such as power generation, telecommunication and attitude and orbit control system (AOCS).
The communication is performed over X (8-8.4 GHz) and K (25.5-27 GHz) bands. K band data rate is ~55 Mbit/s, and it is one-way, to download the data from the spacecraft to the ground. It can be operated for less than 4 hours daily, and it can transfer ~850 Gbit of compressed data in a day. Because it does not have a constant communication channel (but only 4 hours), Euclid has to store all the data in its memory, which is more than 2.6Tbits. X band is used for control and telemetry.
The attitude and orbit control (AOCS) provides a very stable pointing with less than 35 milli-arcseconds during an exposure. The full moon is ~200 milli-arcseconds, so it means approx. it may move maximum 1/6 of the full moon during an exposure lasting almost an hour.
PLM (Payload Module)
Payload Module (PLM) contains the telescope, thermal control system, fine guidance sensor (FGS), and the instruments: VIS and NISP.

PLM with VIS covered in black insulation and NISP covered in gold insulation
(source: NASA Euclid Fact Sheet)
Telescope
Euclid carries a 1.2m Korsch telescope with three anastigmatic (=astigmatic errors are cancelled) mirrors which avoids multiple optical distortions. Its focal length is 24.5m and it has a $0.53\ deg^2$ field-of-view. All of the mirrors are made from silicon carbide (SiC). The primary mirror (M1) is kept below 130K (-143.15C) with a thermal stability better than 50mK (0.05C). The second mirror M2 is mounted on a mechanism that can do focal corrections. The distance between M1 and M2 is 1.756m.

Integrating the telescope (source: euclid.cnes.fr credit: Airbus Defense & Space)

The telescope of Euclid’s PLM in testing (source: euclid.cnes.fr credit: ESA)
Instruments
Euclid has 2 main instruments: VIS (Visible Imager or Visible Instrument) and NISP (Near Infrared Spectrometer and Photometer). These are located on the same optical path. The light from the telescope is reflected from two wide-bandwidth mirrors (FoM1 and FoM2), reflected from mirror M3, enters a (longpass) dichroic beamsplitter plate (~920nm) at the exit pupil of the telescope in front of NISP. The beamsplitter reflects the visible light to a band-pass filter FoM3 which then goes to VIS. The infrared light that passes through the beamsplitter enters NISP.
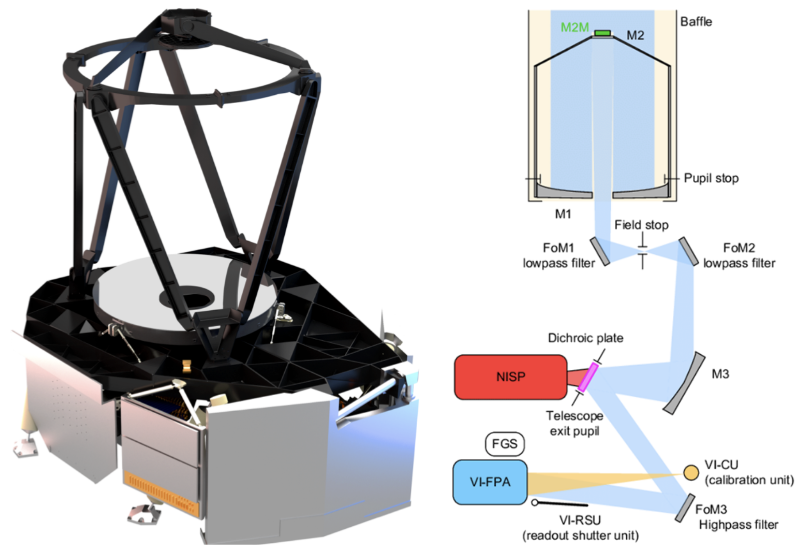
Model and diagram of PLM (source: euclid.cnes.fr credit: ADS Toulouse)
Here is, I think, an accurate 3D drawing of the placement of the instruments. It is upside down, the telescope is connected to the bottom part here (see where the red dashed line coming from):
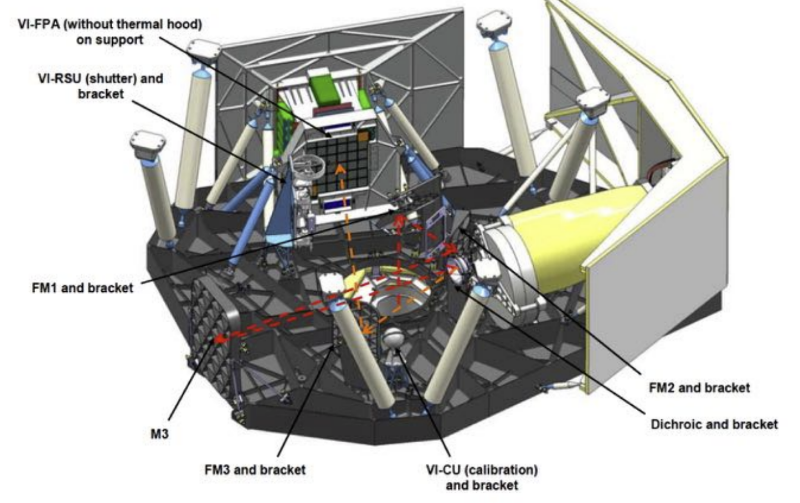
Placement of VIS and NISP (source: Cropper et al. VIS: the visible imager for Euclid)
VIS (Visible Instrument)
VIS is basically a large digital camera. It has 609 million pixels (609MP) in total. Naturally, this is not a single huge sensor, but 36 CCD sensors (made by Teledyne, CCD273-84) arranged in 6x6 matrix. The CCD sensor (also called detector) is back-illuminated and it has 4096x4132 12um pixels. Each pixel covers 0.1 arcsec.
The CCD sensors are read from each corner, so there are 144 channels in total (36x4). The pixels are digitised to 16-bits. Each bit corresponds to 3.4 electrons, and the internal noise is less than 4.4 electrons.
There is only a single broadband filter in front of the CCD, covering the band from 550nm to 900nm. Its operating temperature is -120C, while the temperature of electronics is between 0 and 20C.

A front view of the focal plane with 36 VIS CCDs and 4 Fine Guidance Sensor CCDs
(source: euclid-ec.org, credits: CEA, e2v, Airbus, IAS, APCO)
There is a central data processing for VIS that constructs the image from the pixel data and (lossless) compresses it in 250 seconds. No further processing is performed on the spacecraft. The compressed data from NIS is transferred to ground at 520 Gbit/day.
NISP (Near Infrared Spectrometer and Photometer)
NISP covers the same field of view as VIS, but processes the light between 900 and 2000nm. It contains a detector array consisting of 16 H2RG detectors (made by Teledyne), each having 2040x2040 18um pixels. Each pixel covers 0.3 arcsecond. NISP does both photometry (NISP-P) and slitless spectroscopy (NISP-S).
It is not shown in the diagram of PLM above but NISP also has a calibration unit with 5 LEDs.
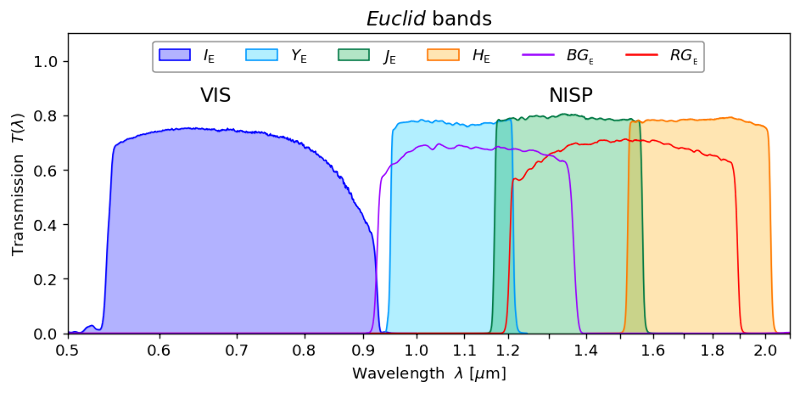
Euclid passbands (source: Euclid Consortium)
The infrared light that passes through the beamsplitter enters a filter wheel (FWA). The filter wheel contains five positions, with three passband filters ($Y_E$, $J_E$, $H_E$ covering approximately 900-1192nm, 1192-1544nm, and 1544-2000nm), a closed position (blocking the light) and an open position for spectroscopy.
After FWA, the light enters a grism wheel (GWA). The grism wheel contains five positions, one “blue” (BGS000) grism covering 920nm-1250nm, three “red” (RGS000, RGS180 and RGS270) grisms covering 1250nm-1850nm, and an open position for photometry. The blue grism is not used for EWS, it is only for EDS. Also, RGS270 grism is not used.
What is a Grism?: It is a combination of a GRating and a prISM. It passes the central wavelength through, while creating a dispersed spectrum around this central wavelength.
The whole instrument can be seen below. The light enters from the corrector lens, passes the filter and the grism wheels, passes the camera lenses, and reaches the focal plane.
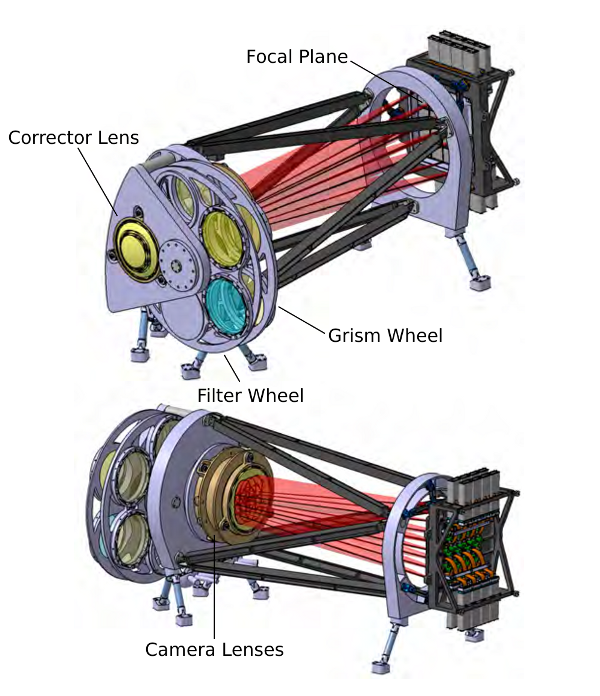
NISP (source: MPIA/EC)
The data from NISP is transferred to ground at 180 Gbit/day.
Launch and Orbit
Euclid spacecraft is launched on a Space X Falcon 9 rocket on 2023/07/01. The spacecraft will operate at the second lagrange point, L2, since it is far from the Sun, the Earth and the Moon to eliminate unwanted effects, but it is still close enough for high-bandwidth communication. 41 minutes after the launch, the Euclid spacecraft is deployed (separated from the rocket) and continues on its transfer orbit to L2.
ESA’s launch broadcast is pretty informative, if you are interested, I recommend watching it.
ESA publishes a live blog post of Euclid’s first months in space.
The Euclid spacecraft will reach to the insertion point (to enter its orbit) approx. 30 days after the launch and then it will travel to its final orbit.
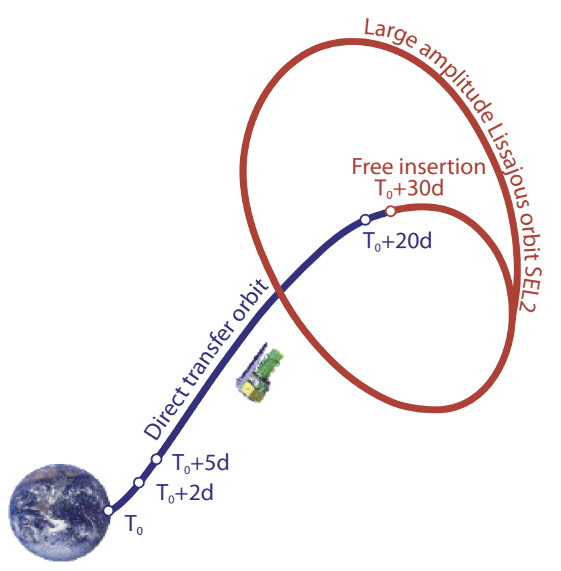
Euclid’s Transfer Orbit (source: R. Scaramella et al.: The Euclid Wide Survey)
Since the orbits around L2 are not stable, orbital station-keeping or trajectory correction manouvre (TCM) is required, that is small corrections are needed to keep the spacecraft on the orbit. Euclid will make TCMs every 30 days.
At its orbit, Euclid will always receive sunlight, no solar eclipse happens. The Earth or the Moon never blocks the sunlight. This is important for the thermal stability of the instruments on Euclid.
Euclid acquires data pointing to a fixed direction (stare mode) and then makes a rotation (slew) to point to the next field (step mode). Because rotations use cold gas, the number of rotations are limited to 950 large and $2.5\times10^5$ small ones. Not surprisingly, this means the EWS should work in adjacent fields as possible.
Lagrange Points
It took me a little while to figure out what the Lagrange point exactly means. Here is my version for an explanation.
First of all, assuming circular orbits, the more closer an object to the Sun, the shorter its orbital period. A Mercury year is 88 days, a Venus year is 225 days, a Mars year is 687 days, and a Jupiter year is 4333 days. So, as long as the spacecraft is not exactly on the Earth’s orbit, it cannot orbit the Sun exactly in one (Earth) year, it should be a bit shorter or longer.
Now lets assume the time is freezed at $t_0$. A Lagrange point at $t_0$ is a point in space where the gravitational forces of two massive (one large, one small) bodies (e.g., Sun-Earth, Sun-Jupiter, Earth-Moon) on a small-body object (e.g., a spacecraft or a satellite) are in equilibrium.
I will say more about what equilibrium means here, but before that lets see what L1 and L2 are. There are always five Lagrange points for such a system with two massive bodies and a small-body, and they are named L1, L2, L3, L4, and L5. L1 and L2 is important because they are close to the Earth (easy to reach) and in direct line of sight (faster communications). Because L1 has a direct view of the Sun, it is particularly used by the things observing the Sun. Because L2 has a direct view of the space (without the interference of the Sun, the Earth and the Moon), it is particularly used by the things observing the space. As a result, ESA’s SOHO and NASA’s ACE both doing solar research are at L1; whereas, ESA’s Gaia and Euclid, and NASA’s James Webb Telescope are at L2. Saying they are at L1 or L2 does not mean they are staying on the same location. It only means they are orbiting L1 or L2. More about orbiting L2 is in the next section.
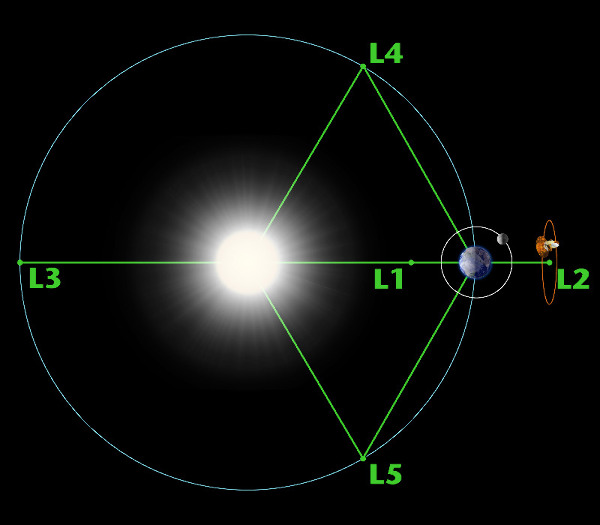
Sun-Earth Lagrange Points (source: solarsystem.nasa.gov)
The equilibrium above means that the small-body object is in an orbit. Being in an orbit, the gravitational forces equal to the centripetal force that keeps the object in the orbit (without this, it would go away, not turn around it). It is not difficult to solve this (see Lagrange Point@wikipedia) to find the distance of L1 and L2 from the earth. The result is that both L1 and L2 is ~1.5 million km from the Earth. The distance between the Sun and the Earth is ~150 million km, and the distance between the Earth and the Moon is ~0.38 million km. L1 and L2 points are 1% of the distance to the Sun, and four times the distance to the Moon.
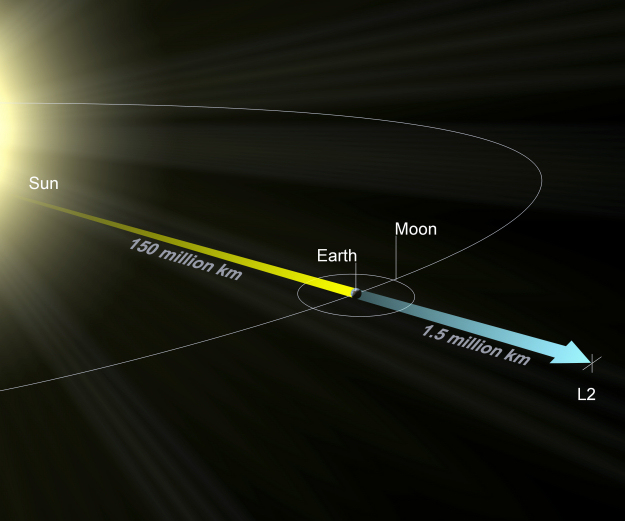
The second lagrange point, L2 (source: ESA)
Just to make it very clear, the small-body (lets say a spacecraft) is not orbiting around the Earth. The spacecraft is orbiting the barycenter (center of mass) of the Sun and the Earth, just like the Earth and the Sun. So, both the Earth and the spacecraft orbiting the Sun, with the same period (1 year). As mentioned before, this is normally impossible, but it is possible here because of the interaction of the two gravitational forces of the Sun and the Earth on the spacecraft.
Extra information about Barycenter: I think some readers may not know this. The Earth actually does not orbit around the Sun (meaning the center of mass of the Sun, a point probably close to the center of the Sun), but actually the center of mass (barycenter) of the Earth and the Sun. Because the mass of the Sun is very large comparing to the Earth, the barycenter is actually inside the Sun. It is very close but still not the center (of mass) of the Sun. Like the Earth orbits the barycenter, the Sun also orbits the barycenter. This is not particular about the Earth or the Sun, it is true for all bodies in space (e.g. Sun-Jupiter, Earth-Moon etc.). When the mass of the bodies are comparable, the barycenter can be a point in space not inside any of the body. For example, the barycenter of the Sun and Jupiter is not inside the Sun. Like two body systems, there is also a barycenter of the entire solar system (including the Sun and all the planets). Due to the movements of the planets, the barycenter is not a fixed point.
I said before lets assume the time is freezed. The reason is that this topic is sometimes shown in a rotating reference frame (around the barycenter with the same period of 1 year). So, the Earth and the lagrange point seems to stay stationary. It just means the Lagrange point orbits the Sun at the same time as the Earth, so they move together. However, there is no stationary lagrange point in 3D, the position of this hypotetical point depends on time, it changes with time as the Earth moves.
Naturally the Earth rotates around its axis every day, and the spacecraft orbits the lagrange point L1 and L2 (not daily, the orbit is actually huge). Because of the rotation of the Earth, the spacecraft cannot always be seen from the same point on the Earth (i.e., the spacecraft at L2 is not geostationary).
Lissajous and Halo L2 Orbits
You may ask how multiple spacecrafts can be at L2, naturally only one thing can be at one point. This is not the only reason but the spacecrafts do not stay at L2, they even do not stay close to L2, but orbit around L2. They orbit both the barycenter (of Sun-Earth) and L2. The orbit at L2 is either a quasi-periodic Lissajous orbit or a periodic Halo orbit. ESA’s previous mission Gaia follows a Lissajous orbit, but James Webb Space Telescope (JWST) is following a Halo orbit. There are some confusing information on the internet about Euclid’s orbit. It is sometimes called Lissajous (wikipedia), sometimes called Lissajous Halo, and sometimes Halo (ESA). I dont know why it is like that, maybe I dont know enough about the topic. However, as far as I can tell it is a Halo orbit like JWST. You can see in the figure below, Lissajous orbit is like moving on the surface of a cylinder, but Halo orbit is just like regular circular orbit.

Orbits of Gaia (yellow), James Web Space Telescope (JWST, blue) and Euclid (white) (taken as a screenshot from Gaia Sky program)
As you can see in the figure above, the Halo orbits are huge (compare it to the Moon’s orbit around the Earth in light purple color), they are more than 1 million km in diameter. The distance between the Moon and the Earth is less than 0.4 million km. The orbital period of Euclid is I think around 6 months.
The three animated gifs below show a simulation of Euclid’s orbit (in purple) as seen in different planes together with the Earth’s orbit (in cyan):

Euclid’s orbit (source: wikipedia)
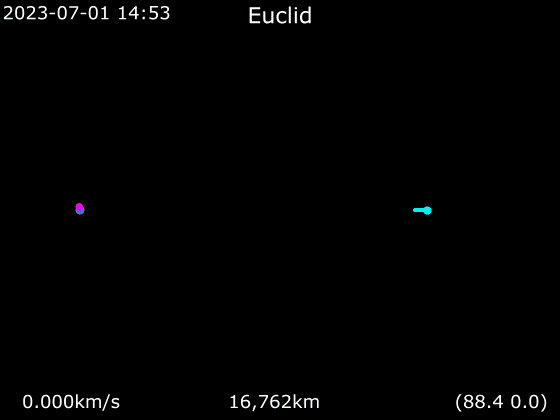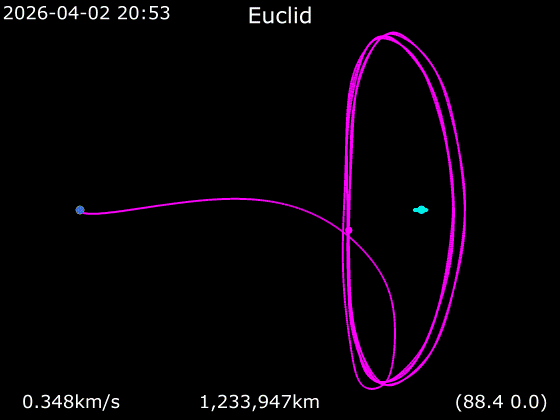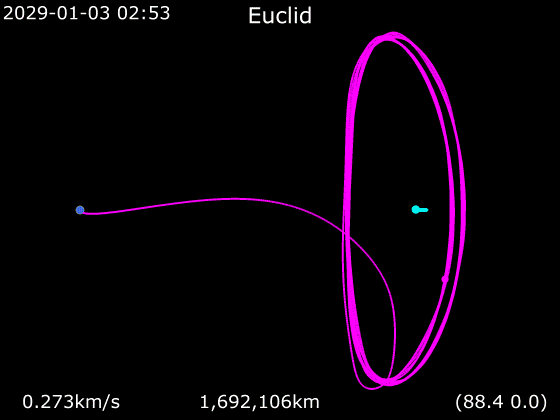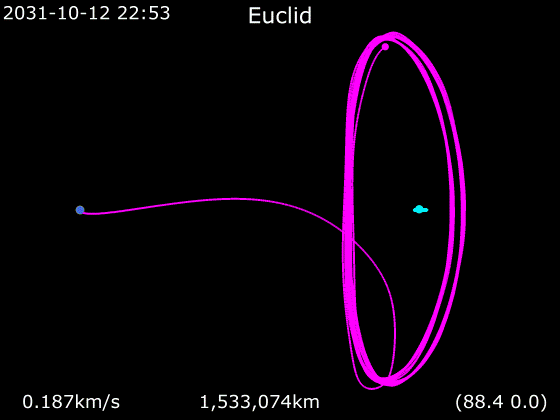
Euclid’s orbit (source: wikipedia)
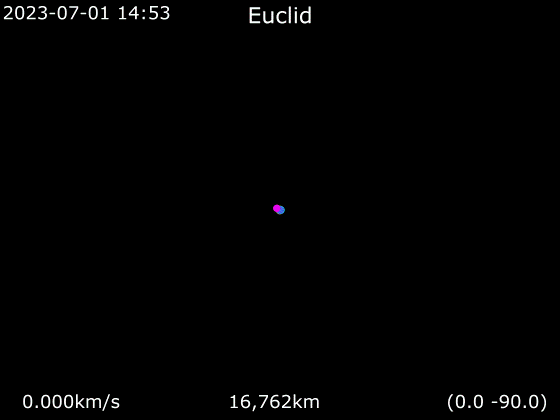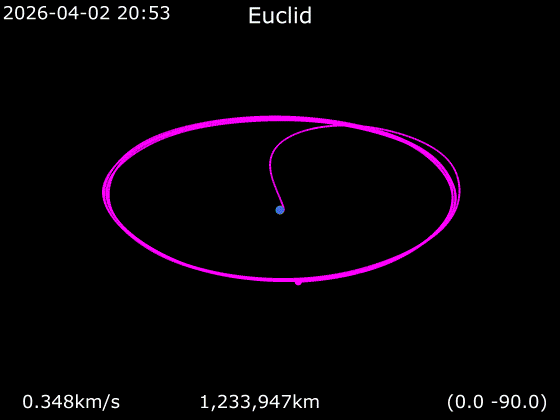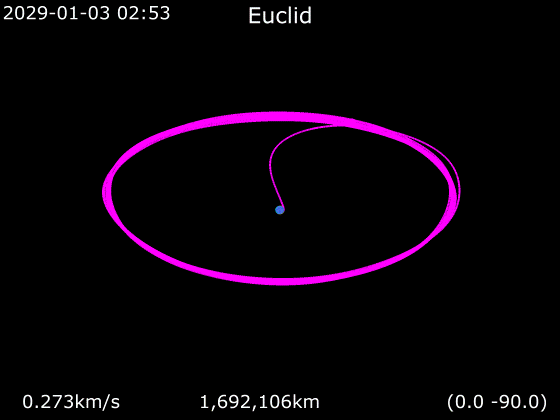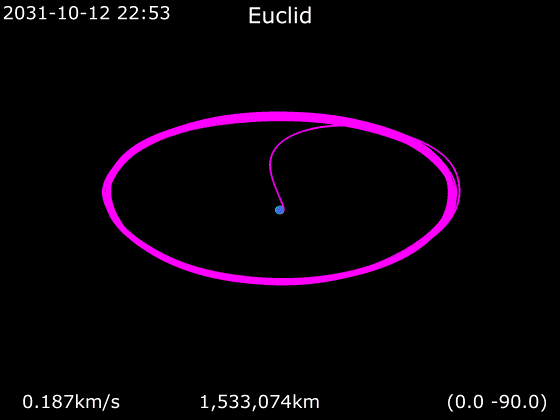
Euclid’s orbit (source: wikipedia)
Ground Segment
ESA has three large 35m antennas almost 120 degrees apart to provide a continous coverage as the Earth rotates. The first is at New Norcia (Australia), the second is at Cebreros (Spain) and the third is at Malargüe (Argentina). These are called Deep Space Antennas (DSA), and called DSA-1, DSA-2 and DSA-3.
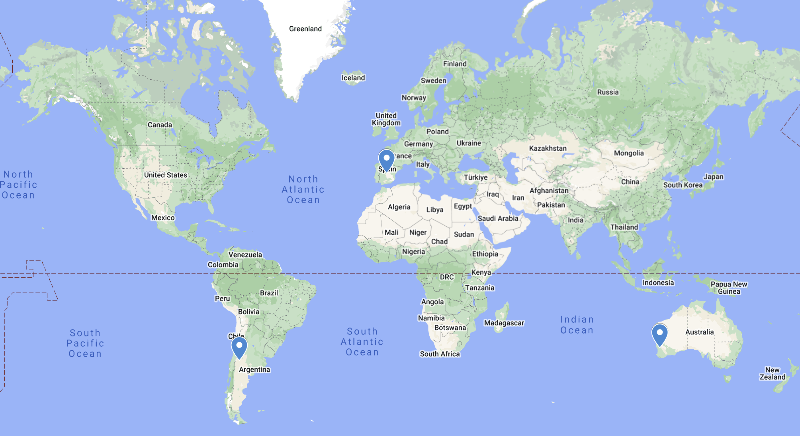
The locations of the ESA Deep Space Antennas in Australia, Spain and Argentina
The antennas are equiped with advanced equipment including cryo-cooled (approx. -260C) low-noise amplifiers. The very low temperature decreases the effects of thermal noise in the electronics.
These three antennas are operated remotely from ESA network operations center (ESOC) in Darmstadt (Germany).
Euclid will have a 4 hour window each day for communication, and either the antenna at Cebreros (DSA-2) or at Malargüe (DSA-3) will be used. Other than these 4 hours, Euclid operates on its own with no communication with the Earth.
When writing this section, I did not realize how big these antennas really are. I was showing my daughter the images below, and then I realized, assuming a floor height of ~3m, the antenna is bigger than a 10-floors building.
The three images below are live webcam images (not auto-refreshing):

Live webcam image of DSA-1 at New Norcia, Australia (source: ESA)

Live webcam image of DSA-2 at Cebreros, Spain (source: ESA)

Live webcam image of DSA-3 at Malargüe, Argentina (source: ESA)
ESA’s Estrack dashboard shows the communication status with Euclid in real-time. I just checked and it shows the last pass of Euclid as tracked by the ground station at MLG (Malargüe) as:
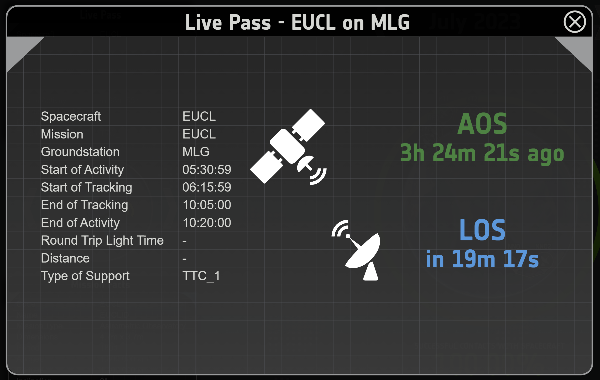
Screenshot (on 2023-07-07 9:46 CET) of Live Pass of Euclid (source: Estrack dashboard)
As it can be seen the activity is less than 5 hours and the tracking is less than 4 hours. Hence, the maximum communication time of Euclid is under 4 hours.
Reference Observation Sequence (ROS)
The total time of Euclid’s mission is divided as below. Naturally, it is not only collecting data for the surveys, but also spending time for calibrations etc.
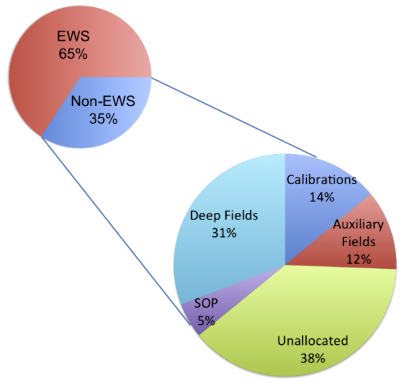
The breakdown of the total time of the Euclid mission (2190 days) for RSD_2021A
(source: Scaramella, R. et al. 2021)
Euclid builds a survey in step-and-stare mode. Step means it moves to the field of view, and stare means it acquires the data while keeping its pointing. Each pointing (each field) is observed 4 times (4 frames are acquired) with a slight dithering (slight offset), so that anything that falls on the gaps of the sensor, also falls on the sensor at least in 3 frames out of 4. After the observation of the last frame, there is a slew (step) movement to the next field of view. So, it basically repeats these steps during a survey:
- acquire frame 1
- dither
- acquire frame 2
- dither
- acquire frame 3
- dither
- acquire frame 4
- slew (to the next field)
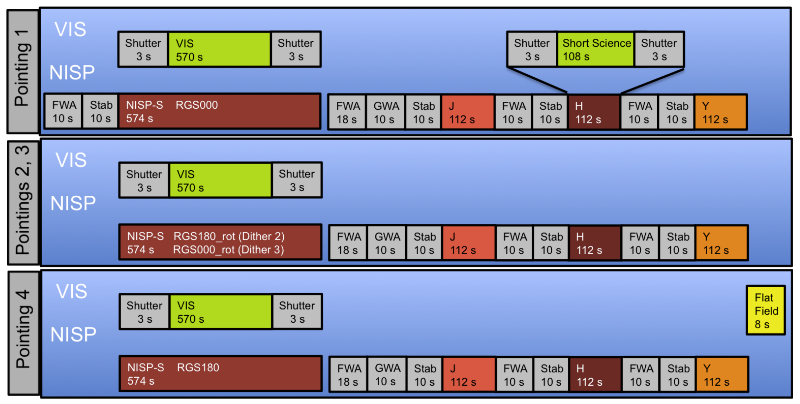
ROS for each field, observing four dithered pointings
(source: R. Scaramella et al.: The Euclid Wide Survey)
For each field, four images are acquired pointing slightly to different directions. At each pointing, VIS and NISP spectral image are acquired simultaneously, both lasting approx. 570 seconds. After that, the grism wheel (GWA) and the filter wheel (FWA) move for the three NISP photometry images, lasting 112 seconds each. During these 112 seconds, VIS acquires bias, flat and other calibration images. Also, in the first pointing, a short 108s exposure of H-band is taken by VIS.
The total duration of ROS is 4214 seconds, slightly over 1 hour. After that, a rotation is performed and most of these rotations are small. The rotation duration is a function of rotation angle, on average it is 182 seconds. A large rotation is approx. 1% of all rotations.
Data Releases
Euclid spacecraft will start its normal function 3 months later (Start/T0) after the launch, after commissioning and performance validation. After early survey operations of 6 months after Start/T0, it will begin the actual survey operations. The demonstration of first data that will contain $50 deg^2$ will be released as a “quality release 1 - Q1” after 14 months (T1=T0+14 months). After a year later, the data will be released to the public, as “data release 1 - DR1” (T1+1 year). DR1 is planned to contain $2500 deg^2$. The next data release DR2 will contain $7500 deg^2$ and will be released in T1+3 years. The final data release DR3 will contain the full survey $~15000 deg^2$ and it will be released T1+6 years. There will also be Q2, Q3 and Q4 at T1+2, T1+4 and T1+5 years.
NASA’a Nancy Grace Roman Space Telescope
NASA is going to launch Nancy Grace Roman Space Telescope possibly in 2027, and its mission also includes investigating the dark energy and matter, similar to Euclid. So, they will complement each other. Comparing to Euclid, Roman will survey a smaller area, about $2000\ deg^2$ or 1/20 of the sky. However, its survey will be in more detail and with more precision. In addition to cosmology, Roman will also make other types of surveys. It will observe only in the infrared bands and it will also be positioned at L2.
Resources
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.